了解 Relax 抽象

Relax 是 Apache TVM Unity 策略中使用的一种图抽象，它有助于端到端地优化 ML 模型。Relax 的主要目标是描述 ML 模型的结构和数据流，包括模型不同部分之间的依赖关系和联系，以及如何在硬件上执行模型。

端到端模型执行

在本章中，我们将使用以下模型作为示例。这是一个两层神经网络，由两个线性运算和 relu 激活组成。

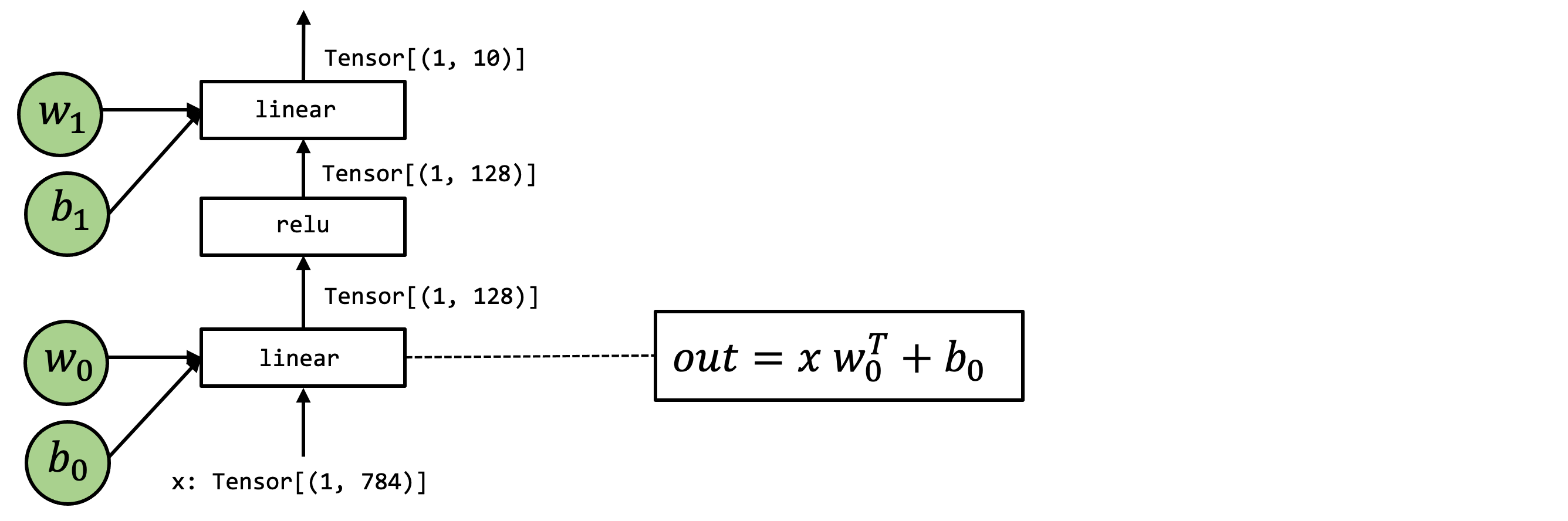
高层操作表示

让我们首先回顾一下该模型的 Numpy 实现。

def numpy_mlp(data, w0, b0, w1, b1):
    lv0 = data @ w0 + b0
    lv1 = np.maximum(lv0, 0)
    lv2 = lv1 @ w1 + b1
    return lv2

上面的示例代码展示了执行端到端模型执行的高层数组操作。当然，我们可以使用 Relax 重写上面的代码，如下所示

from tvm.script import relax as R

@R.function
def relax_mlp(
    data: R.Tensor(("n", 784), dtype="float32"),
    w0: R.Tensor((784, 128), dtype="float32"),
    b0: R.Tensor((128,), dtype="float32"),
    w1: R.Tensor((128, 10), dtype="float32"),
    b1: R.Tensor((10,), dtype="float32"),
) -> R.Tensor(("n", 10), dtype="float32"):
    with R.dataflow():
        lv0 = R.matmul(data, w0) + b0
        lv1 = R.nn.relu(lv0)
        lv2 = R.matmul(lv1, w1) + b1
        R.output(lv2)
    return lv2

底层集成

然而，再次从机器学习编译 (MLC) 的角度来看，我们希望了解这些数组计算的底层细节。

为了说明底层的细节，我们将再次用底层 numpy 编写示例

我们将在必要时使用循环而不是数组函数来演示可能的循环计算。如果可能，我们总是通过 numpy.empty 显式分配数组并在它们之间传递。下面的代码块显示了同一模型的底层 numpy 实现。

def lnumpy_linear(X: np.ndarray, W: np.ndarray, B: np.ndarray, Z: np.ndarray):
    n, m, K = X.shape[0], W.shape[1], X.shape[1]
    Y = np.empty((n, m), dtype="float32")
    for i in range(n):
        for j in range(m):
            for k in range(K):
                if k == 0:
                    Y[i, j] = 0
                Y[i, j] = Y[i, j] + X[i, k] * W[k, j]

    for i in range(n):
        for j in range(m):
            Z[i, j] = Y[i, j] + B[j]


def lnumpy_relu0(X: np.ndarray, Y: np.ndarray):
    n, m = X.shape
    for i in range(n):
        for j in range(m):
            Y[i, j] = np.maximum(X[i, j], 0)

def lnumpy_mlp(data, w0, b0, w1, b1):
    n = data.shape[0]
    lv0 = np.empty((n, 128), dtype="float32")
    lnumpy_matmul(data, w0, b0, lv0)

    lv1 = np.empty((n, 128), dtype="float32")
    lnumpy_relu(lv0, lv1)

    out = np.empty((n, 10), dtype="float32")
    lnumpy_matmul(lv1, w1, b1, out)
    return out

考虑到底层的 NumPy 示例，现在我们准备介绍用于端到端模型执行的 Relax 抽象。下面的代码块显示了该模型的 TVMScript 实现。

@I.ir_module
class Module:
    @T.prim_func(private=True)
    def linear(x: T.handle, w: T.handle, b: T.handle, z: T.handle):
        M, N, K = T.int64(), T.int64(), T.int64()
        X = T.match_buffer(x, (M, K), "float32")
        W = T.match_buffer(w, (K, N), "float32")
        B = T.match_buffer(b, (N,), "float32")
        Z = T.match_buffer(z, (M, N), "float32")
        Y = T.alloc_buffer((M, N), "float32")
        for i, j, k in T.grid(M, N, K):
            with T.block("Y"):
                v_i, v_j, v_k = T.axis.remap("SSR", [i, j, k])
                with T.init():
                    Y[v_i, v_j] = T.float32(0.0)
                Y[v_i, v_j] = Y[v_i, v_j] + X[v_i, v_k] * W[v_k, v_j]
        for i, j in T.grid(M, N):
            with T.block("Z"):
                v_i, v_j = T.axis.remap("SS", [i, j])
                Z[v_i, v_j] = Y[v_i, v_j] + B[v_j]

    @T.prim_func(private=True)
    def relu(x: T.handle, y: T.handle):
        M, N = T.int64(), T.int64()
        X = T.match_buffer(x, (M, N), "float32")
        Y = T.match_buffer(y, (M, N), "float32")
        for i, j in T.grid(M, N):
            with T.block("Y"):
                v_i, v_j = T.axis.remap("SS", [i, j])
                Y[v_i, v_j] = T.max(X[v_i, v_j], T.float32(0.0))

    @R.function
    def main(
        x: R.Tensor(("n", 784), dtype="float32"),
        w0: R.Tensor((784, 256), dtype="float32"),
        b0: R.Tensor((256,), dtype="float32"),
        w1: R.Tensor((256, 10), dtype="float32"),
        b1: R.Tensor((10,), dtype="float32")
    ) -> R.Tensor(("n", 10), dtype="float32"):
        cls = Module
        n = T.int64()
        with R.dataflow():
            lv = R.call_tir(cls.linear, (x, w0, b0), out_sinfo=R.Tensor((n, 256), dtype="float32"))
            lv1 = R.call_tir(cls.relu, (lv0,), out_sinfo=R.Tensor((n, 256), dtype="float32"))
            lv2 = R.call_tir(cls.linear, (lv1, w1, b1), out_sinfo=R.Tensor((b, 10), dtype="float32"))
            R.output(lv2)
        return lv2

上面的代码包含多种函数：原始张量函数 (T.prim_func) 和 R.function (relax 函数)。Relax 函数是一种新型的抽象，表示高层神经网络执行。

请注意，上面的 relax 模块原生支持符号形状，请参阅 main 函数中的张量形状中的 "n" 以及 linear 函数中的 M、N、K。这是 Relax 抽象的一个关键特性，它使编译器能够全局跟踪跨张量运算符和函数调用的动态形状关系。

再次并排查看 TVMScript 代码和底层 numpy 代码并检查相应的元素会很有帮助，我们将详细介绍每个元素。由于我们已经了解了原始张量函数，因此我们将专注于高层执行部分。

Relax 的关键要素

本节将介绍 Relax 抽象的关键要素以及它如何在 ML 编译器中实现优化。

结构信息

结构信息是 Relax 中的一个新概念，它表示 relax 表达式的类型。它可以是 TensorStructInfo、TupleStructInfo 等。在上面的示例中，我们使用 TensorStructInfo（在 TVMScript 中简写为 R.Tensor）来表示输入、输出和中间结果的张量的形状和 dtype。

R.call_tir

R.call_tir 函数是 Relax 中的一个新抽象，它允许在同一 IRModule 中调用原始张量函数。这是 Relax 的一个关键特性，它实现了跨层抽象，从高层神经网络层到低层张量运算。以下面的代码行作为示例

lv = R.call_tir(cls.linear, (x, w0, b0), out_sinfo=R.Tensor((n, 256), dtype="float32"))

为了解释 R.call_tir 的工作原理，让我们回顾一下等效的底层 numpy 操作实现，如下所示

lv0 = np.empty((n, 256), dtype="float32")
lnumpy_linear(x, w0, b0, lv0)

具体来说，call_tir 分配一个输出张量 res，然后将输入和输出传递给 prim_func。在执行 prim_func 后，结果将填充到 res 中，然后我们可以返回结果。

这种约定称为目标传递。其思想是输入和输出在外部显式分配并传递给底层原始函数。这种风格常用于底层库设计，因此高层框架可以处理内存分配决策。请注意，并非所有张量运算都可以用这种风格表示（特别是，有些运算的输出形状取决于输入）。然而，在实践中，如果可能，通常有助于以这种风格编写底层函数。

数据流块

relax 函数中的另一个重要元素是 R.dataflow() 范围注释。

with R.dataflow():
    lv = R.call_tir(cls.linear, (x, w0, b0), out_sinfo=R.Tensor((n, 256), dtype="float32"))
    lv1 = R.call_tir(cls.relu, (lv0,), out_sinfo=R.Tensor((n, 256), dtype="float32"))
    lv2 = R.call_tir(cls.linear, (lv1, w1, b1), out_sinfo=R.Tensor((b, 10), dtype="float32"))
    R.output(lv2)

在我们讨论数据流块之前，让我们首先介绍纯和副作用的概念。如果一个函数满足以下条件，则它是纯函数或无副作用函数

• 它只从其输入读取数据，并通过其输出返回结果

• 它不会更改程序的其他部分（例如递增全局计数器）。

例如，所有 R.call_tir 函数都是纯函数，因为它们仅从其输入读取数据并将输出写入另一个新分配的张量。但是，原地操作不是纯函数，换句话说，它们是有副作用的函数，因为它们会更改现有的中间张量或输入张量。

数据流块是一种标记程序计算图区域的方法。具体来说，在数据流块内，所有操作都必须是无副作用的。在数据流块外部，操作可以包含副作用。

注意

一个常见的疑问是为什么我们需要手动标记数据流块而不是自动推断它们。这种方法有两个主要原因

• 自动推断数据流块可能具有挑战性且不精确，尤其是在处理对打包函数（例如 cuBLAS 集成）的调用时。通过手动标记数据流块，我们使编译器能够准确地理解和优化程序的数据流。

• 许多优化只能应用于数据流块内。例如，融合优化仅限于单个数据流块内的操作。如果编译器错误地推断数据流边界，则可能会错过关键的优化机会，从而可能影响程序的性能。

通过允许手动标记数据流块，我们确保编译器拥有最准确的信息来处理，从而实现更有效的优化。